Jordan Roszmann

I am a mechanical engineer at Babcock Canada and a former sessional lecturer teaching thermodynamics, mechanical design and finite element analysis at UVic. I have two children and divide my time between non-linear dynamic simulations, working on my house and garden, and coaching soccer.
My PhD research was focused on transport phenomena in semiconductor growth, and it involved experiments, thermal and mechanical design, and development of finite element simulations.
Contact Me
Personal:
Jordan Roszmann
Victoria, BC
Canada
250-889-9484
vcard
Professional:
Jordan Roszmann
Design and Systems Engineering
Babcock Canada
Uptown 2
250-889-9484
vcard
I also reluctantly check these occasionally:
Linked-In
Research Gate
Facebook
Publications
| J. Roszmann. Simulation and Growth of Cadmium Zinc Telluride from Small Seeds by the Travelling Heater Method. PhD Dissertation University of Victoria, 2016. |
| J. Roszmann, M. Sekhon, and S. Dost. Measurement of the diffusivity of CdTe in liquid Te at crystal growth temperatures. Journal of Crystal Growth, 411:30 - 3, 2015. [url ] |
| J. Roszmann, S. Dost, and B. Lent. Crystal growth by the travelling heater method using tapered crucibles and applied rotating magnetic field. Crystal Research and Technology, 45(8):785 - 790, 2010. [url ] |
| J. Roszmann, Y.C. Liu, S. Dost, B. Lent, S. Grenier, and N. Audet. Use of rotating magnetic field for selenium impurity transport in zone refining of tellurium and cadmium. Fluid Dynamics and Materials Processing, 5(3):231 - 244, 2009. |
| J. Roszmann. Application of rotating magnetic fields to the travelling heater method growth of GaSb and the synthesis of CdTe. Master's thesis, University of Victoria, Canada, 2009. [url] |
| S. Dost, Y.C. Liu, J. Haas, J. Roszmann, S. Grenier, and N. Audet. Effect of applied electric current on impurity transport in zone refining. Journal of Crystal Growth, 307(1):211 - 218, 2007. [DOI | url ] |
| A. Tura, J. Roszmann, J. Dikeos, A. Rowe. Active magnetic regenerator test apparatus. AIP Conference Proceedings, Apr 2006 |
Some Projects I Found Interesting
Travelling Heater Method Growth
My graduate research is on the THM growth of CdTe and CdZnTe. In THM, the semiconducting compounds are dissolved in liquid tellurium rather than melted, resulting in lower thermal stress and better compositional control. The goal of my research was to grow large single crystals of these two materials using small seed crystals, which is not a common practice in THM. Currently crystals are grown at a uniform diameter which requires very large and expensive seeds.
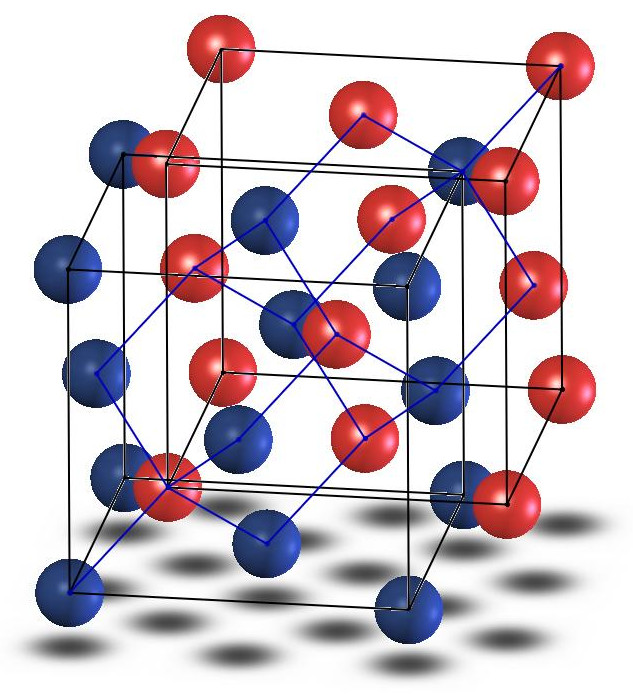
The zincblende materials in this project consist of interpenetrating cubic lattices such that each atom has four nearest neighbours of the other species. (Solidworks)
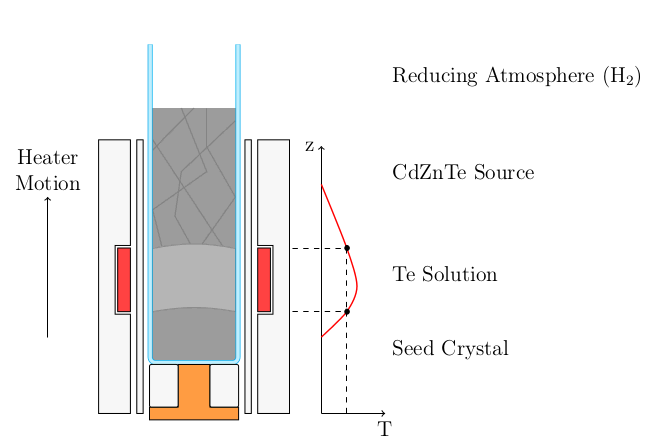
Schematic of a THM growth system. Solid dissolves continuously and is deposited onto a seed crystal. (Tikz)
I have performed dozens of THM experiments using GaSb, CdTe and CdZnTe. Each one required cutting and etching feed materials and glassware, loading and atmosphere control, and then controlled heating and translation in purpose-built furnaces. At the end of each experiment the crystal was removed, cut, polished and etched prior to analysis. In most cases, visual inspection was enough to evaluate the quality of the growth conditions, but I have also used optical microscopy, energy-dispersive electron microscopy and gas-discharge mass spectroscopy to analyze the materials. Apart from material handling, most of my experimental contribution has been the design and fabrication of research furnaces and saws, programming of integrated control systems, and implementation of rotating magnetic fields or accelerated ampoule rotation.

A THM ampoule in the clean room prior to processing.

A 25 mm CdTe boule grown from a 10 mm diameter seed.
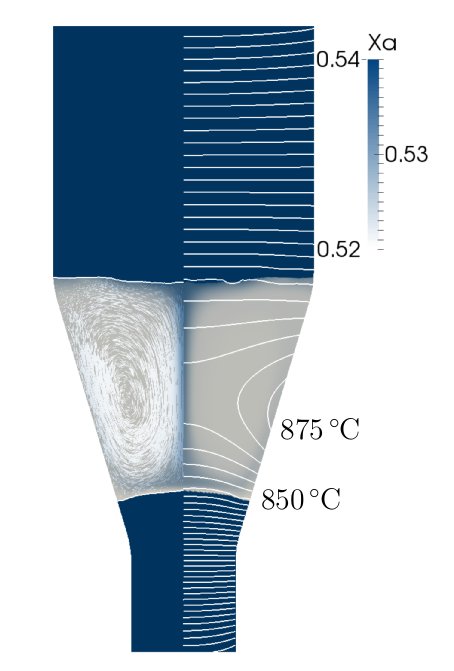
25 mm diameter THM simulation. (Paraview/Tikz)
I also had the pleasure of developing a finite element transport model for the THM system, using a fixed grid algorithm to track the evolution of the dissolution and growth interfaces. The transport regime in THM is strongly advective, requiring a non-linear solution to the momentum (Navier-Stokes), energy and solute transport equations.
Preliminary analysis was done in ANSYS CFX and then Matlab, but in the end a new model was developed from first principles using the Deal.II C++ library. My PhD studies afforded the time to work through the finite element process in detail and develop a unique application which took advantage of templating and parallel processing to give complete control over the solution process. I am grateful for the opportunity to thoroughly geek out for several years on transport modelling and software development.
Zone Refining
Zone refining is an important commercial process for producing very high purity metals. It works because of the composition difference between the solidus and liquidus curves in the equilibrium phase diagrams of mixtures. When a molten zone passes through a solid, impurities are either absorbed or rejected preferentially at the solidification front. This results in migration of the impurities after multiple zone passes and the development of an ultra-pure region in the centre of the ingot. My first project in the crystal growth laboratory was an investigation of zone refining, and with the support of MITACS I spent several months at 5N Plus in Montreal working with their zone refining equipment. Back in Victoria, I applied rotating magnetic fields and forced-air cooling in order to increase temperature gradients and promote mixing and stability of the liquid zones in the zone refining of cadmium.
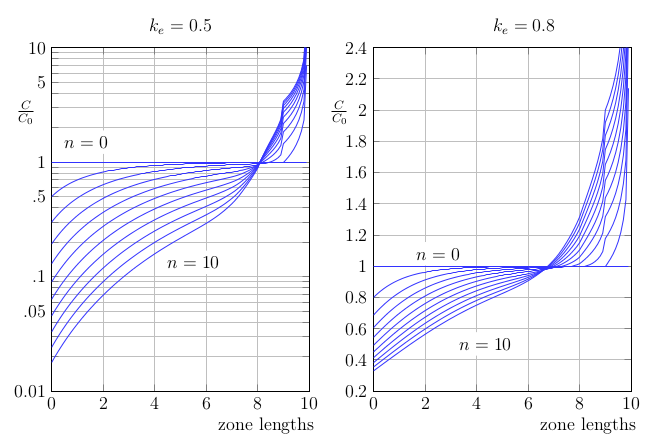
Calculated solute profiles after several zone-refining passes

The zone refining test apparatus at UVic
The phenomenon of solute rejection at an interface is an interesting example of the thermodynamic equilibria discussed in Mech 240. Combining the first and second laws with the definition of the Gibbs free energy, we find the following expression for the rate of entropy generation in a closed system consisting of a two-phase mixture.
\[ T \delta {S}_{gen} = T\operatorname{d}S - \delta Q = T\operatorname{d}S - \operatorname{d}U - p \operatorname{d}V = - \operatorname{d}G - S\operatorname{d}T - V\operatorname{d}p \]
If the system is isothermal and isobaric, then the second law dictates that the Gibbs free energy will decrease until equilibrium is achieved and \(\delta S_{gen}\) vanishes. For an interface at equilibrium, therefore, the total Gibbs free energy of the solid and liquid will be equal. The equilibrium phase diagram is calculated through this condition, taking account of the enthalpies of formation, fusion and reaction for of all constituents as well as the entropies of mixing. When all is taken into account, different equilibrium compositions are found for the solid and liquid phases, which we call the solidus and liquidus concentrations. The ratio of these concentrations, \( k = C_S/C_L\) is called the segregation coefficient and it determines the effectiveness of each zone refining pass.
Refprop
An interesting side project several years ago was for a company that wished to include refrigerant properties from the NIST Chemistry Webbook in an app aimed at the refrigeration service industry. It was very interesting to look through the documentation of REFPROP and recreate the algorithms used to extract the necessary properties from available data. The basic idea is to start with an expressions for the Helmholtz free energy and specific heat as functions of temperature and density and then use numerical differentiation and quadrature to obtain other properties as necessary. We start by non-dimensionalizing terms and dividing the free energy into an ideal gas part and a residual. \[\tau = \frac{T_c}{T}~~~,~~~\delta=\frac{\rho}{\rho_c}~~~,~~~f = \frac{F}{RT} = f^0 + f^r(\tau,\delta)\] Then, we can obtain properties such as pressure or enthalpy. \[p = \rho R T \left( 1 + \delta \frac{\partial f^r}{\partial \delta}\right)\] \[ h = h_0^0 + \int_{T_0}^{T} c_p dT + RT \left(\tau \frac{\partial f^r}{\partial \tau} + \delta \frac{\partial f^r}{\partial \delta} + 1\right) \] Surprisingly little data must be stored. Only the coefficients for calculating \(c_p\) and \(f^r\) are needed in order to fully define a fluid.
Low Temperature Gas Circulator
During my undergraduate studies I spent time in the cryofuels lab at the University of Victoria developing magnetic refrigeration systems. Magnetic refrigeration is based on the magnetocaloric effect. When a paramagnetic material is magnetized, the entropy of its magnetic domains drops. Because the process is adiabatic, this drop in magnetic entropy must be balanced by an increase in thermal entropy, that is a rise in temperature. This magnetocaloric effect can be used to construct a refrigeration cycle analagous to conventional vapour-compression cycles.
- Adiabatic magnetization
- Heat extraction at higher temperature
- Adiabatic demagnetization
- Heat absorption at lower temperature
As a co-op student I contributed to the design of a desktop prototype based on permanent magnets. Most of my time, though, was spent on a low-temperature gas circulator for the active magnetic regenerator test apparatus. The AMRTA uses a 5 T superconducting solenoid to test active regenerators at room temperature and at cryogenic temperatures. The gas circulator connects a room-temperature helium compressor to the cryogenic AMRTA system. The temperature span is sustained by a recuperator and a cold head. I designed the two heat exchangers and the associated tubing and fittings in Solidworks before assembling the system. I also chose, mounted and calibrated sensors and wrote a control system in LabView to monitor the system. This was an excellent undergraduate research project made possible by an NSERC Undergraduate Student Research Award.
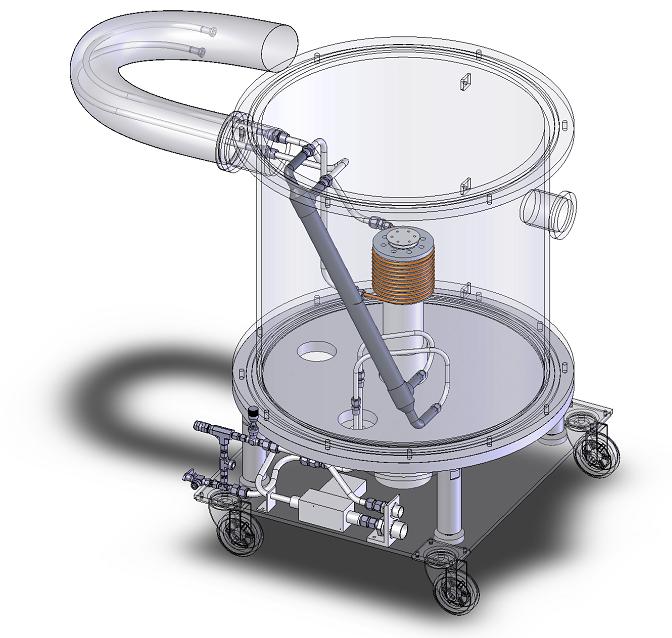
Low temperature gas circulator for cryogenic equipment.
Teaching
I have taught three courses so far with sizes ranging from 48 to 175 students. In the larger classes I made extensive use of Moodle/Course Spaces, iClicker and office hours to maintain a responsive dialogue with my students and tailor the course content to revisit topics that gave trouble early on. My teaching philosophy follows three rules:
- Lectures should give an alternative narrative to the textbook so that students have two perspectives to learn from.
- I consider the course's position within the overall degree program and must help students see what aspects of it will be most useful to them.
- I should listen to students, answer their questions thoroughly and make sure that the answers are available equally to all students.
MECH 240 - Thermodynamics
My approach to thermodynamics is to minimize the time spent getting students over the initial shock of engaging with a very foreign type of physics. This gives time later for ideas to come into focus. To this end, we all worked extremely hard for the first three weeks with
- Gamified rote-learning of vocabulary and core concepts
- Motivating the global, scalar analysis based on energy/entropy by contrasting with local, vector analysis based on momentum
- Getting through standard polytropic processes to the efficiency of Otto and Diesel cycles within the first three weeks.
Core take-aways
At the end of mech 240, I want every student to understand the origin, application and implications of the combined first and second laws. Any system from which we want to extract work must give off thermal energy to regulate its total entropy. Once this heat output is calculated, the recoverable work can be expressed from the energy and entropy balances in terms of mass and energy flows and the temperature at which heat leaves the system.
\[ \dot{W}_{out} = \sum\limits_{in}\dot{W}
+ \sum\limits_{in}\dot{m}(h - Ts)
- \sum\limits_{out}\dot{m}(h - Ts)
+ \sum\limits_{in}Q_{\alpha} \left(1 - \frac{T_{out}}{T_\alpha}\right)- T_{out}\dot{S}_{gen} \]
The primary skill acquired in mech 240 is to identify a thermodynamic system, see the way it exchanges heat and work, and use balance laws to quantify the net work it produces or absorbs. We do this with internal combustion engines, with pumps, compressors, nozzles, diffusers and turbines, with Brayton and Rankine engines and with heat pumps and refrigerators. Because of the hard work done early in mech 240, we also had time to look briefly at jet engines, desalinators, chimneys, and fuel cells, and to briefly explore the concept of free energy and its importance to chemical reactions and equilibria.
Apart from acquiring appreciation for the first and second laws, much of mech 240 is dedicated to building practical knowledge of thermodynamic data and how to look it up and apply it. By introducing complete ideal gas cycles in the first month students had plenty of practice tabulating properties and calculating first and second-law efficiencies for standard engines.
Fun questions
Some of these are from students and some were posed on exams
Why can buoyancy never be used to create a cyclical engine?
When we first learn about the net buoyancy force on submerged objects, it is tempting to try to construct an engine to exploit it. For example, maybe we can fill balloons at the bottom of a tank and then empty them for the return trip. This won't work for two reasons. Most importantly, if we consider the tank as a thermodynamic system then if net work is extracted from the tank, it must be balanced by heat flux into the tank. This heat will raise the tank's entropy unless there is negative entropy generation in the tank, which is forbidden by the second law. Also, the buoyancy is a net normal surface force acting on the submerged body. Over they course of a full cycle of any submerged body, careful calculation will find that the net work done by such forces is zero. Except in simple cases, the calculation of these surface forces is much more complicated than the first argument based on entropy, so an understanding of thermodynamics tells us that this engine cannot work much more simply than a detailed inspection of its mode of operation.
Given that life on earth becomes more complex over time, does evolution violate the the second law?
No. The earth constantly absorbs heat from the sun in warm regions and radiates heat into space from colder regions. Even if we assume that the earth's energy content is approximately constant, the rate of change of the earth's total entropy might not be. \[ \frac{dS}{dt} = \dot{Q}\left( \frac{1}{T_{in}} - \frac{1}{T_{out}}\right) + \dot{S}_{gen}\] Even though the rate of entropy generation must be positive due to random processes such as friction, the total entropy could be going up or down since \( T_{out} < T_{in} \).
Mech 295 - Thermodynamics, Fluid Dynamics and Heat Transfer
In the summer of 2015 I taught mech 295 to electrical engineers. The course covered the same thermodynamics curriculum used in Mech 240, with a few minor simplifications, and then went on to cover internal flow, convection, conduction, log-mean temperature spans in space and time, heat exchangers, lump-capacitance models, extendended surfaces, and radiation. The students who stuck through to the end showed remarkable resilience and a broad grasp of thermal engineering. I think that some mechanical engineering students would benefit from a more integrated approach the thermodynamics and heat transfer.
Where does the log-mean temperature difference come from?
The LMTD can seem like one of many approximations engineers use to same time, but it is in fact an exact result that is at the root of several of the heat transfer relations we reach for frequently. Start with two bodies or streams that exchange heat at an average rate \(\bar{q}\) so that the hot one becomes cooler and the cool one becomes hotter. The temperature changes are in proportion to their respective heat capacities. The analysis is the same whether the heat transfer takes place over time \(t\) or distance \(L\). \[ \bar{q}L = m_h c_{ph} (T_1-T_2) = m_c c_{pc} (t_2 - t_1)\] We can also look at a differential amount of heat exchange, associated with a differential temperature change that takes place over a differential time (or distance). \[\delta q = m_h c_{ph} dT = UA\Delta T dt\] This small heat transfer results in a change in the temperature difference between the objects. \[ d(\Delta T) = dT - dt = \delta q \left(\frac{-1}{m_h c_{ph}}-\frac{1}{m_c c_{pc}}\right) = \frac{-1}{m_h c_{ph}}\left( 1 + \frac{t_2 - t_1}{T_1 - T_2}\right) UA\Delta T dx\], Separating the differential equation is separable, \[ \frac{d(\Delta T)}{\Delta T} = \frac{UA}{m_h c_{ph}} \left( \frac{T_2 - t_2 - T_1 + t_1}{T_1-T_2} \right) ds\] and integrating we can substitute end-point temperatures for the time-case or for parallel flow. \[ \operatorname{ln}\left(\frac{T_2-t_2}{T_1-t_1}\right) = ((T_2-t_2) - (T_1-t_1))UA \frac{L}{m_h c_{ph}(T_1-T_2)} \] Finally, we look back to the start at our definition for the average heat flux, and recover the expected expression for the LMTD. \[ \bar{q} = UA \frac{(T_2 - t_2) - (T_1 - t_1)}{\operatorname{ln}\left( \frac{T_2-t_2}{T_1-t_1} \right)}\]
MECH 493 - Design of Thermo-Fluid Systems
I have taught design of thermo-fluid systems for several years as a TA and sessional instructor. This is primarily a project course with teams of four senior students designing systems that involve fluid dynamics and heat transfer. The course makes use of analysis that the students have already learned, but there have always been problem sets and quizzes to reinforce their prior knowledge. In recent years I added lectures on the economic optimization of piping systems and heat exchangers.
Student teams are often interested in designing
- Hydronic systems
- Fuel cells, batteries and thermal management
- Building heating loads
- Geothermal and solar thermal systems
- Thermal energy storage
- Distillation, brewing, and desalination
- Cryogenic energy systems
- Radiators, condensers, heat exchangers
Some Nice Things People Have Said
I wish I could have more of your vivid and inspirational lectures. Thermodynamics is not a new topic to me since I was somehow exposed to this part when I was taking PHYS 111, but you were the one who made it charming and aroused my interest in it.
Amazing Instructor, made the course very interesting and easy to learn. A lot of assignments given, but it was helpful at the end of the semester.
I couldn't ignore my top Google hit: Rate my Professor
The early comments reflect the very intense effort I demanded in the first three weeks of Mech 240 and Mech 295, particularly the first time I taught them. Most students found relief later in the courses. I put tremendous time and effort into helping students through difficult concepts, and I am gratified to know when it is appreciated.